Cóż za układ równań liniowych. Jak znaleźć rozwiązania ogólne i szczególne układu równań liniowych
Badanie układu liniowych równań agebraicznych (SLAE) pod kątem spójności oznacza sprawdzenie, czy układ ten ma rozwiązania, czy też ich nie ma. Cóż, jeśli istnieją rozwiązania, wskaż, ile ich jest.
Będziemy potrzebować informacji z tematu „Układ liniowych równań algebraicznych. Pojęcia podstawowe. Macierzowa forma zapisu”. W szczególności potrzebne są pojęcia takie jak macierz układu i macierz układu rozszerzonego, gdyż na nich opiera się sformułowanie twierdzenia Kroneckera-Capelliego. Tradycyjnie macierz układu będzie oznaczona literą $A$, a rozszerzona macierz układu literą $\widetilde(A)$.
Twierdzenie Kroneckera-Capelliego
Układ liniowych równań algebraicznych jest spójny wtedy i tylko wtedy, gdy stopień macierzy układu jest równy rządowi rozszerzonej macierzy układu, tj. $\rang A=\rang\widetilde(A)$.
Przypomnę, że układ nazywamy wspólnym, jeśli ma co najmniej jedno rozwiązanie. Twierdzenie Kroneckera-Capelliego mówi, co następuje: jeśli $\rang A=\rang\widetilde(A)$, to istnieje rozwiązanie; jeśli $\rang A\neq\rang\widetilde(A)$, to ten SLAE nie ma rozwiązań (niespójny). Odpowiedź na pytanie o liczbę tych rozwiązań daje wniosek z twierdzenia Kroneckera-Capelliego. Przy formułowaniu wniosku stosuje się literę $n$, która jest równa liczbie zmiennych danego SLAE.
Wniosek z twierdzenia Kroneckera-Capelliego
- Jeśli $\rang A\neq\rang\widetilde(A)$, wówczas SLAE jest niespójny (nie ma rozwiązań).
- Jeśli $\rang A=\rang\widetilde(A)< n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
- Jeżeli $\rang A=\rang\widetilde(A) = n$, to SLAE jest określone (ma dokładnie jedno rozwiązanie).
Należy pamiętać, że sformułowane twierdzenie i jego wniosek nie wskazują, jak znaleźć rozwiązanie SLAE. Za ich pomocą można jedynie dowiedzieć się, czy takie rozwiązania istnieją, czy nie, a jeśli istnieją, to ile.
Przykład nr 1
Przeglądaj SLAE $ \left \(\begin(aligned) & -3x_1+9x_2-7x_3=17;\\ & -x_1+2x_2-4x_3=9;\\ & 4x_1-2x_2+19x_3=-42. \end(aligned )\right.$ dla zgodności. Jeśli SLAE jest kompatybilny, podaj liczbę rozwiązań.
Aby sprawdzić istnienie rozwiązań danego SLAE, korzystamy z twierdzenia Kroneckera-Capelliego. Będziemy potrzebować macierzy układu $A$ i rozszerzonej macierzy układu $\widetilde(A)$, napiszemy je:
$$ A=\left(\begin(tablica) (ccc) -3 i 9 i -7 \\ -1 i 2 i -4 \\ 4 i -2 i 19 \end(array) \right);\; \widetilde(A)=\left(\begin(array) (ccc|c) -3 i 9 &-7 i 17 \\ -1 i 2 i -4 i 9\\ 4 i -2 i 19 i -42 \end(tablica) \right). $$
Musimy znaleźć $\rang A$ i $\rang\widetilde(A)$. Można to zrobić na wiele sposobów, niektóre z nich są wymienione w sekcji Ranking matrycy. Do badania takich układów stosuje się zazwyczaj dwie metody: „Obliczanie rangi macierzy z definicji” lub „Obliczanie rangi macierzy metodą przekształceń elementarnych”.
Metoda numer 1. Obliczanie rang z definicji.
Zgodnie z definicją ranga to najwyższy rząd minorów macierzy, wśród których jest przynajmniej jeden różny od zera. Zwykle badanie rozpoczyna się od nieletnich pierwszego rzędu, ale tutaj wygodniej jest od razu przystąpić do obliczania molla trzeciego rzędu macierzy $A$. Elementy drugorzędne trzeciego rzędu znajdują się na przecięciu trzech wierszy i trzech kolumn omawianej macierzy. Ponieważ macierz $A$ zawiera tylko 3 wiersze i 3 kolumny, to element podrzędny trzeciego rzędu macierzy $A$ jest wyznacznikiem macierzy $A$, tj. $\Delta A$. Do obliczenia wyznacznika stosujemy wzór nr 2 z tematu „Wzory na obliczanie wyznaczników drugiego i trzeciego rzędu”:
$$ \Delta A=\lewo| \begin(tablica) (ccc) -3 i 9 i -7 \\ -1 i 2 i -4 \\ 4 i -2 i 19 \end(tablica) \right|=-21. $$
Zatem istnieje moll trzeciego rzędu macierzy $A$, który nie jest równy zero. Niemożliwe jest skonstruowanie drobnej czwartego rzędu, ponieważ wymaga ona 4 wierszy i 4 kolumn, a macierz $A$ ma tylko 3 wiersze i 3 kolumny. Zatem najwyższy rząd nieletnich macierzy $A$, wśród których jest przynajmniej jeden nierówny zero, wynosi 3. Zatem $\rang A=3$.
Musimy także znaleźć $\rang\widetilde(A)$. Przyjrzyjmy się strukturze macierzy $\widetilde(A)$. Do prostej macierzy $\widetilde(A)$ znajdują się elementy macierzy $A$ i okazało się, że $\Delta A\neq 0$. W rezultacie macierz $\widetilde(A)$ ma moll trzeciego rzędu, który nie jest równy zero. Nie możemy skonstruować nieletnich czwartego rzędu macierzy $\widetilde(A)$, więc wnioskujemy: $\rang\widetilde(A)=3$.
Ponieważ $\rang A=\rang\widetilde(A)$, to zgodnie z twierdzeniem Kroneckera-Capelliego układ jest niesprzeczny, tj. ma rozwiązanie (przynajmniej jedno). Aby wskazać liczbę rozwiązań, bierzemy pod uwagę, że nasz SLAE zawiera 3 niewiadome: $x_1$, $x_2$ i $x_3$. Ponieważ liczba niewiadomych wynosi $n=3$, wnioskujemy: $\rang A=\rang\widetilde(A)=n$, zatem zgodnie z wnioskiem z twierdzenia Kroneckera-Capelliego układ jest określony, tj. ma unikalne rozwiązanie.
Problem został rozwiązany. Jakie wady i zalety ma ta metoda? Najpierw porozmawiajmy o zaletach. Po pierwsze, musieliśmy znaleźć tylko jeden wyznacznik. Następnie od razu wyciągnęliśmy wniosek dotyczący liczby rozwiązań. Zazwyczaj standardowe standardowe obliczenia dają układy równań, które zawierają trzy niewiadome i mają unikalne rozwiązanie. W przypadku takich układów metoda ta jest bardzo wygodna, gdyż z góry wiemy, że istnieje rozwiązanie (w przeciwnym razie przykładu nie byłoby w standardowych obliczeniach). Te. wystarczy, że pokażemy istnienie rozwiązania w większości w szybki sposób. Po drugie, obliczona wartość wyznacznika macierzy układu (tj. $\Delta A$) przyda się później: gdy zaczniemy rozwiązywać dany układ metodą Cramera lub wykorzystując macierz odwrotną.
Jednak metoda obliczania rangi jest z definicji niepożądana, jeśli macierz układu $A$ jest prostokątna. W takim przypadku lepiej zastosować drugą metodę, która zostanie omówiona poniżej. Dodatkowo, jeśli $\Delta A=0$, to nie możemy nic powiedzieć o liczbie rozwiązań danego niejednorodnego SLAE. Być może SLAE ma nieskończoną liczbę rozwiązań, a może nie ma ich wcale. Jeśli $\Delta A=0$, wymagane są dodatkowe badania, co często jest kłopotliwe.
Podsumowując to, co zostało powiedziane, zauważam, że pierwsza metoda jest dobra dla tych SLAE, których macierz systemu jest kwadratowa. Co więcej, sam SLAE zawiera trzy lub cztery niewiadome i jest pobierany ze standardowych standardowych obliczeń lub testów.
Metoda nr 2. Obliczanie rang metodą przekształceń elementarnych.
Metodę tę opisano szczegółowo w odpowiednim temacie. Zaczniemy obliczać rząd macierzy $\widetilde(A)$. Dlaczego macierze $\widetilde(A)$ a nie $A$? Faktem jest, że macierz $A$ jest częścią macierzy $\widetilde(A)$, zatem obliczając rząd macierzy $\widetilde(A)$ jednocześnie znajdziemy rząd macierzy $A$ .
\begin(aligned) &\widetilde(A) =\left(\begin(array) (ccc|c) -3 i 9 &-7 i 17 \\ -1 i 2 i -4 i 9\\ 4 & - 2 i 19 i -42 \end(array) \right) \rightarrow \left|\text(zamień pierwszą i drugą linię)\right| \rightarrow \\ &\rightarrow \left(\begin(array) (ccc|c) -1 i 2 i -4 i 9 \\ -3 i 9 &-7 i 17\\ 4 i -2 i 19 i - 42 \end(array) \right) \begin(array) (l) \phantom(0) \\ II-3\cdot I\\ III+4\cdot I \end(array) \rightarrow \left(\begin (tablica) (ccc|c) -1 i 2 i -4 i 9 \\ 0 i 3 &5 i -10\\ 0 i 6 i 3 i -6 \end(tablica) \right) \begin(tablica) ( l) \phantom(0) \\ \phantom(0)\\ III-2\cdot II \end(array)\rightarrow\\ &\rightarrow \left(\begin(array) (ccc|c) -1 & 2 i -4 i 9 \\ 0 i 3 i 5 i -10\\ 0 i 0 i -7 i 14 \end(array) \right) \end(aligned)
Zredukowaliśmy macierz $\widetilde(A)$ do postaci trapezowej. Na głównej przekątnej wynikowej macierzy $\left(\begin(array) (ccc|c) -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 0 & -7 & 14 \end( array) \right)$ zawiera trzy niezerowe elementy: -1, 3 i -7. Wniosek: rząd macierzy $\widetilde(A)$ wynosi 3, tj. $\rang\widetilde(A)=3$. Dokonując transformacji elementami macierzy $\widetilde(A)$, jednocześnie przekształcaliśmy elementy macierzy $A$ znajdujące się przed linią. Macierz $A$ również zostaje zredukowana do postaci trapezowej: $\left(\begin(array) (ccc) -1 & 2 & -4 \\ 0 & 3 &5 \\ 0 & 0 & -7 \end(array) \prawo)$. Wniosek: rząd macierzy $A$ również wynosi 3, tj. $\zadzwonił A=3$.
Ponieważ $\rang A=\rang\widetilde(A)$, to zgodnie z twierdzeniem Kroneckera-Capelliego układ jest niesprzeczny, tj. ma rozwiązanie. Aby wskazać liczbę rozwiązań, bierzemy pod uwagę, że nasz SLAE zawiera 3 niewiadome: $x_1$, $x_2$ i $x_3$. Ponieważ liczba niewiadomych wynosi $n=3$, wnioskujemy: $\rang A=\rang\widetilde(A)=n$, zatem zgodnie z wnioskiem z twierdzenia Kroneckera-Capelliego układ jest zdefiniowany, tj. ma unikalne rozwiązanie.
Jakie są zalety drugiej metody? Główną zaletą jest jego wszechstronność. Nie ma dla nas znaczenia, czy macierz układu jest kwadratowa, czy nie. Ponadto faktycznie przeprowadziliśmy transformacje do przodu metody Gaussa. Pozostało tylko kilka kroków i moglibyśmy znaleźć rozwiązanie tego SLAE. Szczerze mówiąc, bardziej podoba mi się ta druga metoda niż pierwsza, ale wybór jest kwestią gustu.
Odpowiedź: Podany SLAE jest spójny i zdefiniowany.
Przykład nr 2
Przeglądaj SLAE $ \left\( \begin(aligned) & x_1-x_2+2x_3=-1;\\ & -x_1+2x_2-3x_3=3;\\ & 2x_1-x_2+3x_3=2;\\ & 3x_1- 2x_2+5x_3=1;\\ & 2x_1-3x_2+5x_3=-4. \end(aligned) \right.$ dla zgodności.
Rzędy macierzy układu i macierzy układu rozszerzonego wyznaczymy metodą przekształceń elementarnych. Rozszerzona macierz systemowa: $\widetilde(A)=\left(\begin(array) (ccc|c) 1 i -1 i 2 i -1\\ -1 i 2 i -3 i 3 \\ 2 i -1 & 3 & 2 \\ 3 & -2 & 5 & 1 \\ 2 & -3 & 5 & -4 \end(array) \right)$. Znajdźmy wymagane rangi, przekształcając rozszerzoną macierz układu:

Rozbudowana macierz układu zostaje zredukowana do postaci schodkowej. Jeśli macierz zostanie sprowadzona do postaci rzutowej, wówczas jej ranga będzie równa liczbie niezerowych wierszy. Dlatego $\ zadzwonił A = 3 $. Macierz $A$ (do prostej) sprowadza się do postaci trapezowej i ma rząd 2, $\rang A=2$.

Ponieważ $\rang A\neq\rang\widetilde(A)$, to zgodnie z twierdzeniem Kroneckera-Capelliego układ jest niespójny (tj. nie ma rozwiązań).
Odpowiedź: System jest niespójny.
Przykład nr 3
Przeglądaj SLAE $ \left\( \begin(aligned) & 2x_1+7x_3-5x_4+11x_5=42;\\ & x_1-2x_2+3x_3+2x_5=17;\\ & -3x_1+9x_2-11x_3-7x_5=-64 ;\\ & -5x_1+17x_2-16x_3-5x_4-4x_5=-90;\\ & 7x_1-17x_2+23x_3+15x_5=132. \end(aligned) \right.$ dla zgodności.
Rozszerzona macierz systemu ma postać: $\widetilde(A)=\left(\begin(array) (ccccc|c) 2 & 0 & 7 & -5 & 11 & 42\\ 1 & -2 & 3 & 0 & 2 & 17 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0, 15 i 132 \end(array) \right)$. Zamieńmy pierwszy i drugi wiersz tej macierzy tak, aby pierwszy element pierwszego wiersza stał się jednym: $\left(\begin(array) (ccccc|c) 1 & -2 & 3 & 0 & 2 & 17\\ 2 i 0 i 7 i -5 i 11 i 42 \\ -3 i 9 i -11 i 0 i -7 i -64 \\ -5 i 17 i -16 i -5 i -4 i -90 \\ 7 & -17 i 23 & 0 & 15 & 132 \end(array) \right)$.

Rozciągniętą macierz układu i macierz samego układu sprowadziliśmy do postaci trapezowej. Ranga rozszerzonej macierzy układu jest równa trzy, ranga macierzy układu jest również równa trzy. Ponieważ system zawiera $n=5$ niewiadomych, tj. $\rang\widetilde(A)=\zadzwonił A< n$, то согласно следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Odpowiedź: System jest niepewny.
W drugiej części przyjrzymy się przykładom, które często są uwzględniane w standardowych obliczeniach lub testy w matematyce wyższej: badanie spójności i rozwiązanie SLAE w zależności od wartości parametrów w nim zawartych.
Przykład 1. Znajdź rozwiązanie ogólne i rozwiązanie szczególne układuRozwiązanie Robimy to za pomocą kalkulatora. Zapiszmy rozszerzone i główne macierze: 
Główna macierz A oddzielona jest linią przerywaną. Nieznane układy zapisujemy na górze, pamiętając o możliwości przestawienia wyrazów w równaniach układu. Wyznaczając rangę macierzy rozszerzonej, jednocześnie znajdujemy rangę macierzy głównej. W macierzy B pierwsza i druga kolumna są proporcjonalne. Z dwóch kolumn proporcjonalnych tylko jedna może wpaść w moll podstawowy, zatem przesuńmy np. pierwszą kolumnę poza linię przerywaną z przeciwległym znakiem. Dla systemu oznacza to przeniesienie terminów z x 1 do prawa strona równania. 
Sprowadźmy macierz do postaci trójkątnej. Będziemy pracować tylko z wierszami, gdyż pomnożenie wiersza macierzy przez liczbę różną od zera i dodanie go do innego wiersza dla układu oznacza pomnożenie równania przez tę samą liczbę i dodanie go przez inne równanie, co nie zmienia rozwiązania układu system. Pracujemy z pierwszym wierszem: pomnóż pierwszy wiersz macierzy przez (-3) i dodaj kolejno do drugiego i trzeciego wiersza. Następnie pomnóż pierwszą linię przez (-2) i dodaj do czwartej. 
Druga i trzecia linia są proporcjonalne, dlatego jedną z nich, na przykład drugą, można przekreślić. Jest to równoznaczne z przekreśleniem drugiego równania układu, ponieważ jest konsekwencją trzeciego. 
Teraz pracujemy z drugą linią: pomnóż ją przez (-1) i dodaj do trzeciej. 
Moll kropkowany ma najwyższy rząd (spośród możliwych minorów) i jest niezerowy (it równy produktowi elementy na głównej przekątnej), a ten drugorzędny należy zarówno do macierzy głównej, jak i macierzy rozszerzonej, zatem rangA = rangB = 3.
Drobny  jest podstawowe. Zawiera współczynniki dla niewiadomych x 2 , x 3 , x 4 , co oznacza, że niewiadome x 2 , x 3 , x 4 są zależne, a x 1 , x 5 są wolne.
jest podstawowe. Zawiera współczynniki dla niewiadomych x 2 , x 3 , x 4 , co oznacza, że niewiadome x 2 , x 3 , x 4 są zależne, a x 1 , x 5 są wolne.
Przekształćmy macierz, pozostawiając po lewej stronie jedynie bazę mniejszą (co odpowiada punktowi 4 powyższego algorytmu rozwiązania). 
Układ o współczynnikach tej macierzy jest równoważny układowi pierwotnemu i ma postać

Stosując metodę eliminacji niewiadomych znajdujemy: ![]() , ,
, ,
Otrzymaliśmy relacje wyrażające zmienne zależne x 2, x 3, x 4 poprzez wolne x 1 i x 5, czyli znaleźliśmy rozwiązanie ogólne: 
Przypisując dowolne wartości wolnym niewiadomym otrzymujemy dowolną liczbę rozwiązań cząstkowych. Znajdźmy dwa konkretne rozwiązania:
1) niech x 1 = x 5 = 0, następnie x 2 = 1, x 3 = -3, x 4 = 3;
2) wstaw x 1 = 1, x 5 = -1, następnie x 2 = 4, x 3 = -7, x 4 = 7.
Znaleziono więc dwa rozwiązania: (0,1,-3,3,0) – jedno rozwiązanie, (1,4,-7,7,-1) – drugie rozwiązanie.
Przykład 2. Sprawdź kompatybilność, znajdź ogólne i jedno szczególne rozwiązanie dla systemu 
Rozwiązanie. Przekształćmy pierwsze i drugie równanie, aby mieć jedynkę w pierwszym równaniu i napiszmy macierz B. 
Zera w czwartej kolumnie otrzymujemy operując na pierwszym wierszu: 
Teraz uzyskujemy zera w trzeciej kolumnie za pomocą drugiej linii: 
 Trzecia i czwarta linia są proporcjonalne, więc jedną z nich można przekreślić bez zmiany rangi:
Trzecia i czwarta linia są proporcjonalne, więc jedną z nich można przekreślić bez zmiany rangi:
Pomnóż trzecią linię przez (–2) i dodaj do czwartej: 
Widzimy, że szeregi macierzy głównej i rozszerzonej są równe 4, a stopień pokrywa się z liczbą niewiadomych, dlatego układ ma unikalne rozwiązanie:
;
x 4 = 10- 3x 1 – 3x 2 – 2x 3 = 11.
Przykład 3. Sprawdź system pod kątem kompatybilności i znajdź rozwiązanie, jeśli istnieje. 
Rozwiązanie. Tworzymy rozbudowaną matrycę systemu. 
 Przekształcamy pierwsze dwa równania tak, aby w lewym górnym rogu znajdowała się liczba 1:
Przekształcamy pierwsze dwa równania tak, aby w lewym górnym rogu znajdowała się liczba 1:
Mnożąc pierwszą linię przez (-1) i dodając ją do trzeciej: 
Pomnóż drugą linię przez (-2) i dodaj ją do trzeciej: 
System jest niespójny, ponieważ w macierzy głównej otrzymaliśmy wiersz składający się z zer, który przy znalezieniu rangi jest przekreślany, natomiast w macierzy rozszerzonej pozostaje ostatni wiersz, czyli r B > r A .
Ćwiczenia. Zbadaj ten układ równań pod kątem zgodności i rozwiąż go za pomocą rachunku macierzowego.
Rozwiązanie
Przykład. Udowodnić zgodność układu równań liniowych i rozwiązać go na dwa sposoby: 1) metodą Gaussa; 2) Metoda Cramera. (wpisz odpowiedź w formie: x1,x2,x3)
Rozwiązanie :doc :doc :xls
Odpowiedź: 2,-1,3.
Przykład. Podano układ równań liniowych. Udowodnij jego zgodność. Znajdź rozwiązanie ogólne układu i jedno rozwiązanie szczególne.
Rozwiązanie
Odpowiedź: x 3 = - 1 + x 4 + x 5 ; x 2 = 1 - x 4 ; x 1 = 2 + x 4 - 3x 5
Ćwiczenia. Znajdź rozwiązania ogólne i szczegółowe każdego układu.
Rozwiązanie. Przeanalizujmy ten układ, korzystając z twierdzenia Kroneckera-Capelliego.
Zapiszmy rozszerzone i główne macierze:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Tutaj macierz A jest wyróżniona pogrubioną czcionką.
Sprowadźmy macierz do postaci trójkątnej. Będziemy pracować tylko z wierszami, gdyż pomnożenie wiersza macierzy przez liczbę różną od zera i dodanie go do innego wiersza dla układu oznacza pomnożenie równania przez tę samą liczbę i dodanie go przez inne równanie, co nie zmienia rozwiązania układu system.
Pomnóżmy pierwszą linię przez (3). Pomnóż drugą linię przez (-1). Dodajmy drugą linię do pierwszej:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Pomnóżmy drugą linię przez (2). Pomnóż trzecią linię przez (-3). Dodajmy trzecią linię do drugiej:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Pomnóż drugą linię przez (-1). Dodajmy drugą linię do pierwszej:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Wybrany moll ma najwyższy rząd (z możliwych minorów) i jest niezerowy (jest równy iloczynowi elementów na odwrotnej przekątnej), a ten minor należy zarówno do macierzy głównej, jak i rozszerzonej, zatem rang( A) = rang(B) = 3 Ponieważ ranga macierzy głównej jest równa rangi macierzy rozszerzonej, to system współpracuje.
Ten drobny element jest podstawowy. Zawiera współczynniki dla niewiadomych x 1 , x 2 , x 3 , co oznacza, że niewiadome x 1 , x 2 , x 3 są zależne (podstawowe), a x 4 , x 5 są wolne.
Przekształćmy macierz, pozostawiając po lewej stronie tylko moll podstawy.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
27x 3 =
- x 2 + 13x 3 = - 1 + 3x 4 - 6x 5
2x 1 + 3x 2 - 3x 3 = 1 - 3x 4 + 2x 5
Stosując metodę eliminacji niewiadomych znajdujemy:
Otrzymaliśmy relacje wyrażające zmienne zależne x 1 , x 2 , x 3 poprzez wolne x 4 , x 5 , czyli znaleźliśmy rozwiązanie ogólne:
x 3 = 0
x 2 = 1 - 3x 4 + 6x 5
x 1 = - 1 + 3x 4 - 8x 5
niepewny, ponieważ ma więcej niż jedno rozwiązanie.
Ćwiczenia. Rozwiązać układ równań.
Odpowiedź:x 2 = 2 - 1,67x 3 + 0,67x 4
x 1 = 5 - 3,67 x 3 + 0,67 x 4
Przypisując dowolne wartości wolnym niewiadomym otrzymujemy dowolną liczbę rozwiązań szczegółowych. System jest niepewny
Układ równań liniowych jest sumą n równań liniowych, z których każde zawiera k zmiennych. Jest napisane tak:
Wielu, spotykając się po raz pierwszy z wyższą algebrą, błędnie uważa, że liczba równań musi koniecznie pokrywać się z liczbą zmiennych. W algebrze szkolnej zwykle tak się dzieje, ale w przypadku wyższej algebry, ogólnie rzecz biorąc, nie jest to prawdą.
Rozwiązaniem układu równań jest ciąg liczb (k 1, k 2, ..., k n), który jest rozwiązaniem każdego równania układu, czyli: podstawiając do tego równania zamiast zmiennych x 1, x 2, ..., x n otrzymujemy poprawną równość liczbową.
Zatem rozwiązanie układu równań oznacza znalezienie zbioru wszystkich jego rozwiązań lub udowodnienie, że zbiór ten jest pusty. Ponieważ liczba równań i liczba niewiadomych mogą się różnić, możliwe są trzy przypadki:
- System jest niespójny, tj. zbiór wszystkich rozwiązań jest pusty. Dość rzadki przypadek, który można łatwo wykryć niezależnie od metody zastosowanej do rozwiązania systemu.
- System jest spójny i zdeterminowany, tj. ma dokładnie jedno rozwiązanie. Wersja klasyczna, dobrze znany od czasów szkolnych.
- System jest spójny i nieokreślony, tj. ma nieskończenie wiele rozwiązań. To najtrudniejsza opcja. Nie wystarczy wskazać, że „system ma nieskończony zbiór rozwiązań” – trzeba opisać, jak ten zbiór jest zbudowany.
Zmienną x i nazywamy dozwoloną, jeśli występuje tylko w jednym równaniu układu i ma współczynnik równy 1. Innymi słowy, w innych równaniach współczynnik zmiennej x i musi być równy zero.
Jeśli w każdym równaniu wybierzemy jedną dozwoloną zmienną, otrzymamy zbiór dozwolonych zmiennych dla całego układu równań. Sam system napisany w tej formie będzie również nazywany rozwiązanym. Ogólnie rzecz biorąc, jeden i ten sam oryginalny system można sprowadzić do różnych dozwolonych, ale na razie się tym nie przejmujemy. Oto przykłady dozwolonych systemów:

Obydwa systemy są rozwiązywane w odniesieniu do zmiennych x 1 , x 3 i x 4 . Jednakże z takim samym sukcesem można argumentować, że drugi system jest rozwiązany w odniesieniu do x 1, x 3 i x 5. Wystarczy przepisać ostatnie równanie do postaci x 5 = x 4.
Rozważmy teraz bardziej ogólny przypadek. Miejmy w sumie k zmiennych, z których r jest dozwolone. Możliwe są wtedy dwa przypadki:
- Liczba dozwolonych zmiennych r jest równa całkowitej liczbie zmiennych k: r = k. Otrzymujemy układ k równań, w którym r = k dopuszczalnych zmiennych. Taki system jest wspólny i określony, ponieważ x 1 = b 1, x 2 = b 2, ..., x k = b k;
- Liczba dozwolonych zmiennych r jest mniejsza niż całkowita liczba zmiennych k: r< k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Zatem w powyższych systemach zmienne x 2, x 5, x 6 (dla pierwszego systemu) i x 2, x 5 (dla drugiego) są dowolne. Przypadek, w którym istnieją zmienne wolne, lepiej jest sformułować jako twierdzenie:
Uwaga: to bardzo ważny punkt! W zależności od tego, jak napiszesz wynikowy system, ta sama zmienna może być dozwolona lub bezpłatna. Większość nauczycieli matematyki na poziomie wyższym zaleca zapisywanie zmiennych w porządku leksykograficznym, tj. indeks rosnący. Nie masz jednak obowiązku stosowania się do tej porady.
Twierdzenie. Jeżeli w układzie n równań dopuszczalne są zmienne x 1, x 2, ..., x r oraz x r + 1, x r + 2, ..., x k są wolne, to:
- Jeśli ustalimy wartości zmiennych wolnych (x r + 1 = t r + 1, x r + 2 = t r + 2, ..., x k = t k), a następnie znajdziemy wartości x 1, x 2, ..., x r, otrzymujemy jedną z decyzji.
- Jeśli w dwóch rozwiązaniach wartości zmiennych wolnych są zbieżne, to wartości zmiennych dozwolonych również są zbieżne, tj. rozwiązania są równe.
Jakie jest znaczenie tego twierdzenia? Aby otrzymać wszystkie rozwiązania rozwiązanego układu równań, wystarczy wyizolować zmienne swobodne. Następnie przypisanie do wolnych zmiennych różne znaczenia, otrzymamy gotowe rozwiązania. To wszystko - w ten sposób można uzyskać wszystkie rozwiązania systemu. Nie ma innych rozwiązań.
Wniosek: rozwiązany układ równań jest zawsze spójny. Jeśli liczba równań w rozwiązanym układzie jest równa liczbie zmiennych, układ będzie określony; jeśli jest mniejszy, będzie nieokreślony.
I wszystko byłoby dobrze, ale pojawia się pytanie: jak uzyskać rozwiązany z pierwotnego układu równań? Do tego istnieje
- Systemy M równania liniowe z N nieznany.
Rozwiązywanie układu równań liniowych- to jest taki zbiór liczb ( x 1 , x 2 , …, x rz), po podstawieniu do każdego z równań układu otrzymuje się poprawną równość.
Gdzie a ij , ja = 1, …, m; j = 1, …, n— współczynniki systemowe;
b ja , ja = 1, …, m- wolni członkowie;
x jot, jot = 1, …, n- nieznany.
Powyższy układ można zapisać w postaci macierzowej: A X = B,


Gdzie ( A|B) jest główną macierzą układu;
A— rozbudowana matryca systemu;
X— kolumna niewiadomych;
B— kolumna wolnych członków.
Jeśli macierz B nie jest macierzą zerową ∅, to taki układ równań liniowych nazywa się niejednorodnym.
Jeśli macierz B= ∅, wówczas ten układ równań liniowych nazywa się jednorodnym. Układ jednorodny ma zawsze rozwiązanie zerowe (trywialne): x 1 = x 2 = …, x n = 0.
Wspólny układ równań liniowych jest układem równań liniowych, który ma rozwiązanie.
Niespójny układ równań liniowych jest nierozwiązywalnym układem równań liniowych.
Pewien układ równań liniowych jest układem równań liniowych, który ma unikalne rozwiązanie.
Nieokreślony układ równań liniowych jest układem równań liniowych o nieskończonej liczbie rozwiązań. - Układy n równań liniowych z n niewiadomymi
Jeśli liczba niewiadomych jest równa liczbie równań, wówczas macierz jest kwadratowa. Wyznacznik macierzy nazywany jest głównym wyznacznikiem układu równań liniowych i jest oznaczony symbolem Δ.
Metoda Cramera do rozwiązywania systemów N równania liniowe z N nieznany.
Reguła Cramera.
Jeżeli główna wyznacznika układu równań liniowych nie jest równa zeru, to układ jest spójny i zdefiniowany, a jedyne rozwiązanie oblicza się za pomocą wzorów Cramera:
gdzie Δ i są wyznacznikami otrzymanymi z głównego wyznacznika układu Δ poprzez zastąpienie I kolumnę do kolumny wolnych członków. . - Układy m równań liniowych z n niewiadomymi
Twierdzenie Kroneckera–Capelliego.
Aby dany układ równań liniowych był spójny, konieczne i wystarczające jest, aby stopień macierzy układu był równy rządowi rozszerzonej macierzy układu, zadzwonił(Α) = zadzwonił(Α|B).
Jeśli zadzwonił(Α) ≠ zadzwonił(Α|B), to układ oczywiście nie ma rozwiązań.
Jeśli zadzwonił(Α) = zadzwonił(Α|B), to możliwe są dwa przypadki:
1) ranga (Α) = n(liczba niewiadomych) – rozwiązanie jest unikalne i można je otrzymać korzystając ze wzorów Cramera;
2) ranga (Α)< n - istnieje nieskończenie wiele rozwiązań. - Metoda Gaussa do rozwiązywania układów równań liniowych

Stwórzmy rozszerzoną macierz ( A|B) danego układu ze współczynników niewiadomych i prawych stron.
Metoda Gaussa, czyli metoda eliminowania niewiadomych, polega na redukcji rozszerzonej macierzy ( A|B) używając elementarnych przekształceń w swoich wierszach do widok po przekątnej(do widoku trójkątnego z góry). Wracając do układu równań, wszystkie niewiadome są określone.
Elementarne przekształcenia ciągów obejmują:
1) zamień dwie linie;
2) pomnożenie ciągu przez liczbę inną niż 0;
3) dodanie kolejnego ciągu do ciągu pomnożonego przez dowolną liczbę;
4) wyrzucenie linii zerowej.
Odpowiada rozszerzonej macierzy zredukowanej do postaci diagonalnej układ liniowy, równoważny temu, którego rozwiązanie nie nastręcza trudności. . - Układ jednorodnych równań liniowych.
Układ jednorodny ma postać:
odpowiada to równaniu macierzowemu X = 0.
1) System jednorodny jest zawsze spójny, ponieważ r(A) = r(A|B), zawsze istnieje rozwiązanie zerowe (0, 0, …, 0).
2) Aby układ jednorodny miał rozwiązanie niezerowe, jest to konieczne i wystarczające r = r(A)< n , co jest równoważne Δ = 0.
3) Jeśli R< n , to oczywiście Δ = 0, wtedy powstają wolne niewiadome do 1 , do 2 , …, do nr-r, układ ma nietrywialne rozwiązania, a jest ich nieskończenie wiele.
4) Rozwiązanie ogólne X Na R< n można zapisać w postaci macierzowej w następujący sposób:
X = do 1 X 1 + do 2 X 2 + … + do n-r X n-r,
gdzie są rozwiązania X 1 , X 2 , …, X n-r tworzą podstawowy układ rozwiązań.
5) Z podstawowego układu rozwiązań można otrzymać rozwiązanie ogólne układ jednorodny: ,
,
jeśli ustawimy kolejno wartości parametrów równe (1, 0, …, 0), (0, 1, …, 0), …, (0, 0, …, 1).
Rozbudowa rozwiązania ogólnego w zakresie podstawowego układu rozwiązań jest zapisem rozwiązania ogólnego w postaci kombinacji liniowej rozwiązań należących do układu podstawowego.
Twierdzenie. Aby układ liniowych równań jednorodnych miał rozwiązanie niezerowe, konieczne i wystarczające jest, aby Δ ≠ 0.
Jeśli więc wyznacznik Δ ≠ 0, to układ ma rozwiązanie jednoznaczne.
Jeśli Δ ≠ 0, to układ liniowych równań jednorodnych ma nieskończoną liczbę rozwiązań.
Twierdzenie. Aby układ jednorodny miał rozwiązanie niezerowe, jest to konieczne i wystarczające r(A)< n .
Dowód:
1) R nie może być więcej N(Rząd macierzy nie przekracza liczby kolumn lub wierszy);
2) R< n , ponieważ Jeśli r = n, to główna wyznacznika układu Δ ≠ 0 i zgodnie ze wzorami Cramera istnieje jednoznaczne rozwiązanie trywialne x 1 = x 2 = … = x n = 0, co jest sprzeczne z warunkiem. Oznacza, r(A)< n .
Konsekwencja. W celu uzyskania jednorodnego systemu N równania liniowe z N niewiadome miały niezerowe rozwiązanie, konieczne i wystarczające jest, aby Δ = 0.
Układ m równań liniowych z n niewiadomymi zwany systemem formy
Gdzie ij I b ja (I=1,…,M; B=1,…,N) to kilka znanych liczb, i x 1 ,…,x n– nieznany. W wyznaczaniu współczynników ij pierwszy indeks I oznacza numer równania, a drugi J– liczba niewiadomych, przy której stoi ten współczynnik.
Współczynniki niewiadomych zapiszemy w postaci macierzy 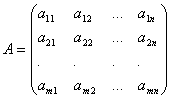 , który nazwiemy macierz układu.
, który nazwiemy macierz układu.
Liczby po prawej stronie równań to b 1 ,…,b m są nazywane wolni członkowie.
Całość N takty muzyczne do 1 ,…,c n zwany decyzja danego układu, jeżeli każde równanie układu staje się równością po podstawieniu do niego liczb do 1 ,…,c n zamiast odpowiednich niewiadomych x 1 ,…,x n.
Naszym zadaniem będzie znalezienie rozwiązań dla systemu. W takim przypadku mogą wystąpić trzy sytuacje:
Układ równań liniowych, który ma co najmniej jedno rozwiązanie nazywa się wspólny. W przeciwnym razie, tj. jeśli system nie ma rozwiązań, nazywa się go nie wspólne.
Zastanówmy się, jak znaleźć rozwiązania dla systemu.
METODA MATRYCOWA ROZWIĄZYWANIA UKŁADÓW RÓWNAŃ LINIOWYCH
Macierze umożliwiają krótkie zapisanie układu równań liniowych. Niech będzie dany układ 3 równań z trzema niewiadomymi:

Rozważmy macierz systemu  i macierze kolumny nieznanych i wolnych terminów
i macierze kolumny nieznanych i wolnych terminów 
Znajdźmy pracę
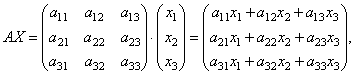
te. w wyniku iloczynu otrzymujemy lewe strony równań tego układu. Następnie korzystając z definicji równości macierzy układ ten można zapisać w postaci
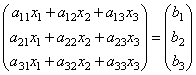 lub krócej A∙X=B.
lub krócej A∙X=B.
Oto macierze A I B są znane, oraz macierz X nieznany. Trzeba go znaleźć, bo... jego elementy są rozwiązaniem tego systemu. To równanie nazywa się równanie macierzowe.
Niech wyznacznik macierzy będzie różny od zera | A| ≠ 0. Następnie równanie macierzowe rozwiązuje się w następujący sposób. Pomnóż obie strony równania po lewej stronie przez macierz A-1, odwrotność macierzy A: . Od A -1 A = E I mi∙X = X, wówczas otrzymujemy rozwiązanie równania macierzowego w postaci X = A -1 B .
Należy zauważyć, że ponieważ macierz odwrotną można znaleźć tylko dla macierzy kwadratowych, metoda macierzowa może rozwiązać tylko te układy, w których liczba równań pokrywa się z liczbą niewiadomych. Jednakże macierzowy zapis układu jest możliwy również w przypadku, gdy liczba równań nie jest równa liczbie niewiadomych, wówczas macierz A nie będzie kwadratowy i dlatego nie da się znaleźć rozwiązania układu w postaci X = A -1 B.
Przykłady. Rozwiązywać układy równań.

REGUŁA CRAMERA
Rozważmy układ 3 równań liniowych z trzema niewiadomymi:

Wyznacznik trzeciego rzędu odpowiadający macierzy układu, tj. złożony ze współczynników niewiadomych,

zwany wyznacznik systemu.
Skomponujmy jeszcze trzy wyznaczniki w następujący sposób: zamień kolejno 1, 2 i 3 kolumny w wyznaczniku D na kolumnę wolnych terminów

Następnie możemy udowodnić następujący wynik.
Twierdzenie (reguła Cramera). Jeżeli wyznacznik układu Δ ≠ 0, to rozpatrywany układ ma jedno i tylko jedno rozwiązanie, a
![]()
Dowód. Rozważmy więc układ trzech równań z trzema niewiadomymi. Pomnóżmy pierwsze równanie układu przez dopełnienie algebraiczne 11 element 11, 2 równanie – włączone 21 i 3. – dalej 31:

Dodajmy te równania:
Przyjrzyjmy się każdemu z nawiasów i prawej stronie tego równania. Według twierdzenia o rozwinięciu wyznacznika w elementach pierwszej kolumny
Podobnie można wykazać, że i .
Wreszcie łatwo to zauważyć 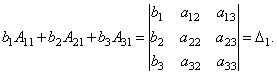
Otrzymujemy zatem równość: .
Stąd, .
Równości i wyprowadza się w podobny sposób, z czego wynika stwierdzenie twierdzenia.
Zauważamy zatem, że jeśli wyznacznik układu Δ ≠ 0, to układ ma rozwiązanie jednoznaczne i odwrotnie. Jeżeli wyznacznik układu jest równy zeru, to układ albo ma nieskończoną liczbę rozwiązań, albo nie ma żadnych rozwiązań, tj. niezgodny.
Przykłady. Rozwiązać układ równań

METODA GAUssa
Omówione wcześniej metody można zastosować do rozwiązania tylko tych układów, w których liczba równań pokrywa się z liczbą niewiadomych, a wyznacznik układu musi być różny od zera. Metoda Gaussa jest bardziej uniwersalna i odpowiednia dla układów o dowolnej liczbie równań. Polega ona na konsekwentnym eliminowaniu niewiadomych z równań układu.
Rozważmy ponownie układ trzech równań z trzema niewiadomymi:
 .
.
Pierwsze równanie pozostawimy bez zmian, a z drugiego i trzeciego wykluczymy terminy zawierające x 1. Aby to zrobić, podziel drugie równanie przez A 21 i pomnóż przez – A 11, a następnie dodaj go do pierwszego równania. Podobnie dzielimy trzecie równanie przez A 31 i pomnóż przez – A 11, a następnie dodaj go do pierwszego. W efekcie oryginalny system przyjmie postać:

Teraz z ostatniego równania eliminujemy termin zawierający x 2. Aby to zrobić, podziel trzecie równanie przez, pomnóż przez drugie i dodaj z drugim. Wtedy będziemy mieli układ równań:
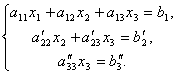
Stąd z ostatniego równania łatwo jest znaleźć x 3, to z drugiego równania x 2 i wreszcie, od 1-go - x 1.
W przypadku stosowania metody Gaussa równania można w razie potrzeby zamienić.
Często zamiast pisać nowy układ równań ograniczają się do napisania rozszerzonej macierzy układu:

a następnie doprowadź go do postaci trójkątnej lub ukośnej za pomocą elementarnych przekształceń.
DO elementarne przemiany macierze obejmują następujące przekształcenia:
- przestawianie wierszy lub kolumn;
- mnożenie ciągu przez liczbę inną niż zero;
- dodanie innych linii do jednej linii.
Przykłady: Rozwiązywać układy równań metodą Gaussa.

Zatem układ ma nieskończoną liczbę rozwiązań.












